This post focuses on Galois’s silicon projects and related research efforts around asynchronous circuit design as we approach the 27th IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC 2021), to be hosted by Galois as a virtual conference September 7–10, 2021.
In a recent blog post, we shared Galois’s interest in asynchronous circuit design. Asynchronous circuit operations are synchronized using local handshake protocols, rather than the global clock signals found in conventional synchronous designs. In the last blog post, we discussed how asynchronous design can overcome bottlenecks in synchronous chip designs and produce more energy-efficient chips by eliminating the need for clock gating and enabling voltage scaling.
So why are synchronous designs still the industry standard? The lack of adoption of asynchronous design stems in part from (1) the lack of robust tools to develop, synthesize, and validate asynchronous circuits; and (2) the difficulties in designing correct and efficient asynchronous circuits. In particular, the bundled data-style asynchronous circuits used in Galois’s projects are subject to subtle bugs in timing assumptions that could lead to data loss.
To combat these issues, Galois has adopted the technique of desynchronization (Cortadella et al. 2006), whereby we start with a synchronous circuit design and make it asynchronous by carefully replacing the global clock signal with a handshaking protocol driven by local controllers. Desynchronization lets us take advantage of industry-standard synthesis and verification tools targeting synchronous circuits, and provides a principled and reliable way to synthesize asynchronous controllers that preserve circuit behavior. Desynchronization can be implemented with various controller designs; Galois’s projects have mostly used Click components (Peeters 2010) and the timing-resilient Blade template (Hand et al. 2015).
But what does it mean for a desynchronized circuit to “preserve the behavior” of its synchronous predecessor? We aim for the property of flow equivalence: every state-holding element in the data path of a desynchronized circuit should store the same sequence of values as in the original synchronous circuit. This allows asynchronous components to operate out of lockstep with the original synchronous circuit, while ensuring no data in the data path is lost or processed multiple times.
The Role of Formal Verification
How can we know whether our particular implementation of desynchronization satisfies flow equivalence? In the process of designing a set of controllers, a hardware engineer will typically reason that flow equivalence is preserved based on invariants that are preserved over the normal course of execution. This reasoning is usually informal, and may or may not be explicitly recorded in notes or code comments. It often relies on subtle timing assumptions that may or may not be explicitly enforced in the circuit design. The reasoning may also build on theoretical results; for example, Cortadella et al. (2006) specified sufficient conditions to ensure flow equivalence based solely on the interactions between neighboring controllers.
Informal reasoning processes are, of course, subject to mistakes and bugs. We discovered a mistake in the proof of Cortadella et al.’s sufficient conditions that led to a slightly different result—their most general desynchronization protocol does not preserve flow equivalence, but the slightly less general rise-decoupled and fall-decoupled protocols do (Paykin et al., 2020).
Formal verification of flow equivalence can reduce or eliminate errors in desynchronized circuits in four specific ways:
- Develop formal models of controllers as state spaces that are closely connected to real-world implementations, yet can be formally analyzed for correctness;
- Explicitly identify the invariants that are required to show flow equivalence, and prove that the formal model satisfies them;
- Explicitly identify previously-implicit timing assumptions, and ensure they are preserved in the formal model; and
- Formally reason about the relationships between neighboring controllers and show these relationships imply flow equivalence.
Formal verification is already used extensively in synchronous hardware design, and has also been applied in asynchronous designs to show hazard-freedom (Nelson, Myers, and Yoneda 2003) and deadlock-freedom (Verbeek, Joosten, and Schmaltz 2013), among other properties.
As with all formal verification, there is some gap between the model and properties being verified and the design that is implemented in silicon. Our models are built out of primitive components, including zero-delay combinational logic blocks, D flip-flops, C elements, and delays to enforce timing constraints. These primitives are then composed to form more complex circuits. The controllers we verify are slight simplifications of the ones used in Galois projects, though they share the same core components.
This work is still in progress and not all theorems have been formally verified. However, the ones that have been do not depend on any unproven hypotheses or implicit assumptions. The models and verified theorems are open source and available on GitHub.
Desynchronization
We start with a sequential circuit as in Fig 1(a), where a global clock drives several D flip-flops with feedback and combinational logic in between. The corresponding desynchronized circuit in Fig 1(b) replaces each flop with a pair of latches, one even and one odd, and replaces the global clock with a set of local clocks, one for each latch, driven by asynchronous controller components. The figure shows four controller components: a token pipeline stage for driving even latches; a non-token pipeline stage for driving odd latches; and split and join elements to account for situations where the data path branches and merges. We focus on the Click controllers used in Galois’s designs, although the particular Click designs we model are slight simplifications of those used in practice.
Figure 1(a). Synchronous circuit. The clouds represent combinational logic blocks. The boxes represent flip-flops, controlled by a central clock, that allow for pipelining and feedback within the circuit.
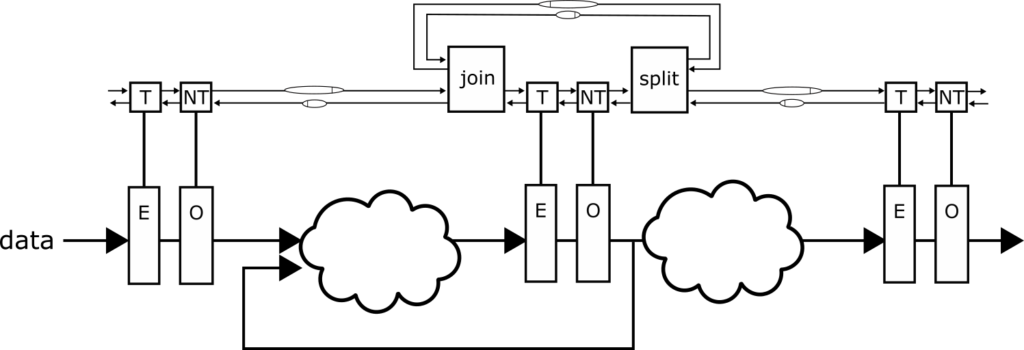
Figure 1(b). Desynchronized circuit. Each flip-flop has been replaced by two latches, denoted even and odd, driven by local controllers that communicate via asynchronous handshake protocols. The ovals on some signal lines, as between the join and split elements, represent delays.
To show flow equivalence, we repaired and formalized Cortadella et al.’s proof and demonstrated that it suffices to show that the rise and fall of neighboring local clocks satisfies the protocol shown in Figure 2, illustrated as a kind of Petri net known as a marked graph. That is, for every even-odd pair of neighboring latches that appears in a circuit (respectively odd-even), the controllers that drive the latches’ local clocks should obey the protocol specified. An event (rise or fall of the latch’s clock) is enabled by a marked graph protocol if all the arrows leading into that event are marked; after an event fires, the markings of the incoming arrows will be removed and new markings will be added to all the outgoing edges from that event.

Figure 2. The fall-decoupled protocol for odd-even and even-odd neighboring latches, respectively. The protocol gives rise to a set of sequences of transition nodes. A transition node is enabled if all incoming arrows into that node have markings. Any enabled node can fire, which removes markings from its incoming arrows and adds markings to each of its outgoing arrows. For example, the protocol on the left gives rise to the sequence [O+ O- E+ E- …] as well as [O+ E+ E- O- …] and [O+ E+ O- E- …].
If this protocol is violated, it could cause data on the data path to be lost. For example, if the control to the left latch (O) rose, fell, and then rose again before the control to the right latch had a chance to rise, the first value latched by O would never be captured by its right neighbor, and the value computed on the data path would be lost. However, we can see that this sequence [O+ O- O+ E+] is not allowed by the protocol in Figure 2.
In the 26th IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC 2020), the Galois team published a paper that showed the mistake in Cortadella et al.’s proof, formalized the notion of flow equivalence, and proved the correctness of the fall-decoupled protocol, as well as two other related protocols.
Modeling and Verification of Click Controllers
With our formalization of flow equivalence and the correctness proof for the fall-decoupled protocol complete, the next step is to show that a particular set of Click components obeys the fall-decoupled protocol, which we do in three stages. First, we model each Click component as a non-deterministic state machine that outputs events on transitions. Inspired by trace theory (Dill 1989), each state machine gives rise to a set of traces reachable from an initial state. These state machines are compositional, in the sense that any two state machines with overlapping domains can be seamlessly combined. Building up each Click component from smaller primitives like combinational logic blocks, flops, and delays (represented in Figure 3 by ovals), we construct a state space that captures the way data flows through a controller, which can then be arbitrarily composed with neighboring controllers.
Formal State Space Models of Circuits
We implemented these state spaces in Coq as an inductive relation based on the tree structure of composition, and implemented automatic tools for reasoning about their composition. This infrastructure will be useful for modeling other circuits as state spaces in Coq for future projects.
Figure 4. A marked graph representation of the key relationships between wires in a non-token and token Click pipeline stage, respectively.
Refining a Controller State Space to a Marked Graph Protocol
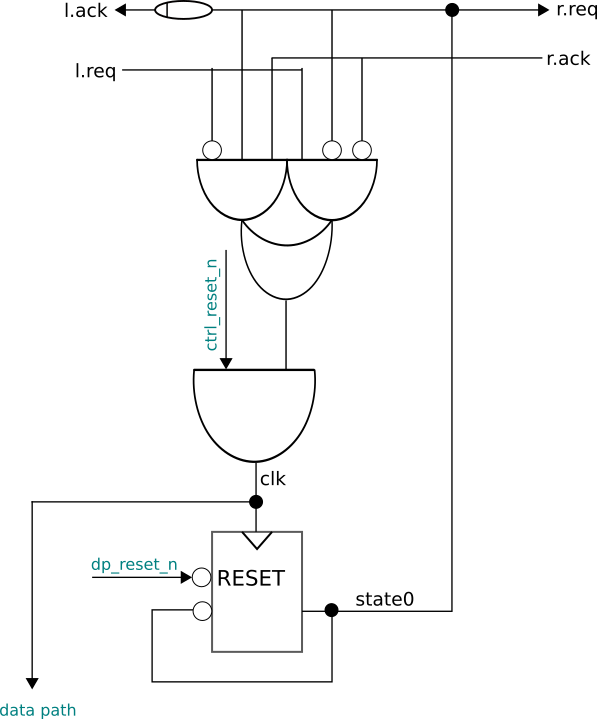
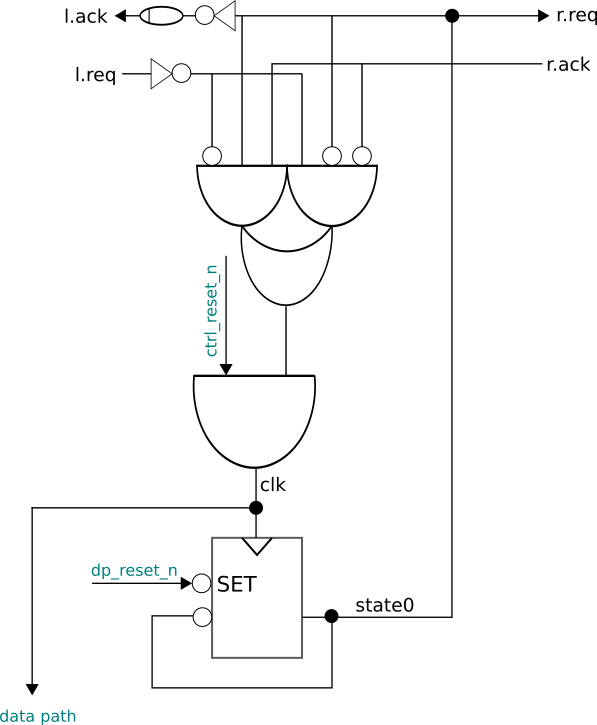
After constructing such a state space for each Click controller component, we reduce it to a marked graph that abstracts away many of the details and highlights the relationship between events on the local clocks and handshake wires (Figure 4). Specifically, we prove that any trace produced by a single Click pipeline stage composed with any environment is also accepted by the corresponding marked graph in Figure 4.
Proving that this correspondence holds requires reasoning about subtle invariants and timing delays that hold in the state space. For example: in a state σ where the right environment is unstable (a request has been sent on r.req but we have not yet received an acknowledgment on r.ack), it must be the case that σ.r.req = σ.state0. That is, even if other parts of the controller are changing as we wait for an acknowledgment from the right, the values of the request line and state0 must stay stable. Such invariants, though fairly obvious to a human observer, are not always easy to prove formally. We found that this was in general a good thing, as humans have a tendency to extrapolate “invariants” that do not always hold. Formal proofs required us to ensure that every corner case was taken into account.
In addition to establishing invariants, we must also relate arbitrary state spaces to marked graphs. To do this, we define a relation σ~m between states σ in the state space and markings m of the marked graph. We then have to show that whenever σ steps to σ’ in the state space via the event e, that same event is enabled in the marking m.
Composing Click Components
All of the results described so far have been formally verified in Coq. The last remaining result has not yet been formalized, but we can sketch the approach here.
We plan to show that no matter how we compose the simplified Click components, neighboring clocks always obey the fall-decoupled protocol. We do this by showing (1) that two neighboring pipeline stages obey the fall-decoupled protocol, and (2) that a pipeline stage connected to a split or join operation still acts like an ordinary pipeline stage if we ignore the extraneous inputs and outputs. Therefore, we can apply the result from (1) even to neighboring controllers that have intermediary splits and joins.
The compositionality of this result means that any circuit constructed via this desynchronization scheme, no matter the size or complexity, exhibits flow equivalence. This distinguishes the result from other formal verification techniques based on model checking whole circuits, which are inherently limited by the size of the circuit being analyzed. In addition, compositionality means that verification would only need to be completed once per desynchronization scheme, and no additional effort would be needed when changes are made to the chip design.
Impact
Why is flow equivalence, and specifically the formalization and verification of flow equivalence, important? In addition to clearly identifying invariants and timing assumptions that might otherwise be left imprecise, this work closes a key gap in the asynchronous workflow by ensuring that our particular implementation of desynchronization does not change the intended behavior of a circuit. This allows hardware designers to rely on higher-level synthesis and verification results of their designs before desynchronization, supported by a wide range of industry tools focused on synchronous designs.
Beyond flow equivalence, much work remains to ensure the correctness of desynchronized designs. For example, flow equivalence does not imply deadlock freedom; a circuit proved to be flow equivalent could still theoretically become stuck waiting for synchronization to occur. In addition, the Click circuits modeled in this work represent a small subset of possible desynchronized designs, and other designs may require different invariants and contain additional asynchronous components such as arbitration blocks. However, by building up a formal system in which we can reason about desynchronized designs, we set the stage for building increasingly high assurance systems and pave the way for further formal reasoning about asynchronous designs.
References
J. Cortadella, A. Kondratyev, L. Lavagno and C. P. Sotiriou, “Desynchronization: Synthesis of Asynchronous Circuits From Synchronous Specifications,” in IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 25, no. 10, pp. 1904-1921, Oct. 2006, doi: 10.1109/TCAD.2005.860958. https://ieeexplore.ieee.org/document/1677680
Dill, David L. Trace theory for automatic hierarchical verification of speed-independent circuits. Vol. 24. Cambridge, MA: MIT Press, 1989.
D. Hand et al., “Blade — A Timing Violation Resilient Asynchronous Template,” 2015 21st IEEE International Symposium on Asynchronous Circuits and Systems, 2015, pp. 21-28, doi: 10.1109/ASYNC.2015.13.
Paykin, Jennifer, Brian Huffman, Daniel M. Zimmerman, and Peter A. Beerel. “Formal Verification of Flow Equivalence in Desynchronized Designs.” In 2020 26th IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC), pp. 54-62. IEEE, 2020.
Peeters, A., Te Beest, F., De Wit, M., & Mallon, W. (2010, May). Click elements: An implementation style for data-driven compilation. In 2010 IEEE Symposium on Asynchronous Circuits and Systems (pp. 3-14). IEEE.
C. A. Nelson, C. J. Myers and T. Yoneda, “Efficient verification of hazard-freedom in gate-level timed asynchronous circuits,” ICCAD-2003. International Conference on Computer Aided Design (IEEE Cat. No.03CH37486), 2003, pp. 424-431, doi: 10.1109/ICCAD.2003.159719.
F. Verbeek, S. Joosten, and J. Schmaltz, “Formal deadlock verification for Click circuits,” in Proc. ASYNC, May 2013, pp. 183–190.